Difference between revisions of "Steady State Examples"
Ilya Kiselev (Talk | contribs) |
Ilya Kiselev (Talk | contribs) |
||
| (4 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
Steady state analysis of the mathematical model comprising system of ordinary differential equations <br> | Steady state analysis of the mathematical model comprising system of ordinary differential equations <br> | ||
<center>dY/dt = f(X, t), Y(0) = Y0 </center> | <center>dY/dt = f(X, t), Y(0) = Y0 </center> | ||
| − | <br>implies finding X_SS and | + | <br>implies finding X_SS and t_SS such that f(X_SS, t) = 0, t > t_SS.<br> |
In BioUML we have two analyses in that regard. | In BioUML we have two analyses in that regard. | ||
| − | + | <ol> | |
| − | + | <li>Algebraic steady state. | |
| − | + | ||
We transform the model to algebraic form<br> F(X, t)=0<br> and solve this algebraic system. | We transform the model to algebraic form<br> F(X, t)=0<br> and solve this algebraic system. | ||
| Line 25: | Line 24: | ||
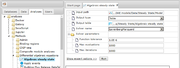
[[File:algebraic_steady_state_analysis_example.png|thumb|Fig.1 Example of Algebraic Steady State Analysis]] | [[File:algebraic_steady_state_analysis_example.png|thumb|Fig.1 Example of Algebraic Steady State Analysis]] | ||
| − | + | <li>Steady state. | |
In this case we simply simulate the model from given initial values Y0 until Y stops changing in time. | In this case we simply simulate the model from given initial values Y0 until Y stops changing in time. | ||
| Line 33: | Line 32: | ||
Additionally user may set which subset of Y variables will be used to check if steady state was found. | Additionally user may set which subset of Y variables will be used to check if steady state was found. | ||
Example of analysis with parameters set is presented on fig. 2. | Example of analysis with parameters set is presented on fig. 2. | ||
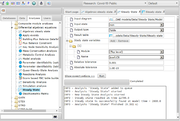
| − | [[ | + | [[File:Steady_state_analysis_example.png|thumb|Fig.2 Example of Steady State Analysis]] |
| + | </ol> | ||
| + | |||
| + | Examples on both analysis can be found at https://ict.biouml.org/bioumlweb/#de=data/Examples/DAE%20models/Data/Steady%20State/ | ||
Latest revision as of 18:09, 19 August 2021
Steady state analysis of the mathematical model comprising system of ordinary differential equations
implies finding X_SS and t_SS such that f(X_SS, t) = 0, t > t_SS.
In BioUML we have two analyses in that regard.
- Algebraic steady state.
We transform the model to algebraic form
F(X, t)=0
and solve this algebraic system. Available solvers:- Levenberg Marquard algorithm
- Newton method
- Conjugate gradient
- KinSolver
Of course this algebaric system may have no solution or more than one solution - in the latter case BioUML will find only one of them.
In order to run Algebraic steady state analysis go to Analysis tab in the repository tree, select Methods then Differential algebraic equations
The very first analysis in the list would be Algebraic steady state analysis
. User should set diagram for which steady state should be found and form of the result (table with parameter values or Simulation result).
Example of analysis with parameters set is presented on the Fig. 1.
Fig.1 Example of Algebraic Steady State Analysis
- Steady state.
In this case we simply simulate the model from given initial values Y0 until Y stops changing in time.
In order to run Steady state analysis go to Analysis tab in the repository tree, select Methods then Differential algebraic equations
And find in the list Steady State user should set diagram for which steady state should be found, form of the result (Diagram in steady state, Simulation result or Table with parameter values). Additionally user may set which subset of Y variables will be used to check if steady state was found. Example of analysis with parameters set is presented on fig. 2.
Fig.2 Example of Steady State Analysis
Examples on both analysis can be found at https://ict.biouml.org/bioumlweb/#de=data/Examples/DAE%20models/Data/Steady%20State/
